creative_2019_28_1_41_47The augmented Zagreb index (AZI) of a graph 
is defined as
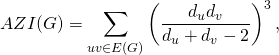
where 
and 
denote set of edges of and degree of the vertex 
in respectively. In this paper we establish some general results and bounds of AZI for certain unicyclic graphs and their corresponding chemical representation. We also obtain some results pertaining to AZI of certain trees.
| Author(s) | Bharali, A., Konch, Nijara |
|---|
Reciprocal distance spectrum of Indu-Bala product of graphs
Some classes of distance spaces as generalized metric spaces: terminology, mappings, fixed points and applications in Theoretical Informatics
Uniqueness of Shift Polynomials and Derivative Sharing Polynomial
Diffeomorphic embedding of Higher-dimensional Hilbert Manifolds into Hilbert spaces
Approximating fixed points of the SP*-iteration for generalized nonexpansive mappings in CAT(0) spaces
Leverage Centrality in Corona Product of Cycle with some Graphs
Some new results on WS-algebras
On Duo Γ-semihyperrings
Comparative Study of Different Vacation Schemes in an Inventory System with Production and Multiple Servers
Isomorphism of Line Graph and Common Neighbourhood Graph
