In this paper, we consider unit speed timelike curves in pseudo-Galilean 
-space 
as curves whose position vectors can be written as linear combination of their Serret-Frenet vectors. We obtain some results of constant ratio curves and give an example of these curves.
Further, we show that there is no 
-constant curve and we obtain some results of 
-constant type of curves in pseudo-Galilean -space 
Constant ratio timelike curves in pseudo-Galilean 3-space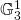
Kişi, İlim, Büyükkütük, Sezgin and Öztürk, Günay
Full PDF
creative_2018_27_1_57_62Additional Information
| Author(s) | Büyükkütük, Sezgin, Kişi, İlim, Öztürk, Günay |
|---|
Recently posted
-
Fuzzy Noetherian Module
-
Simpson Type Tensorial Norm Inequalities for Continuous Functions of Selfadjoint Operators in Hilbert Spaces
-
Leverage Centrality on Barycentric Subdivision of Some Graphs
-
On Prime Ideal Space of a Partially Ordered Ternary Semigroup
-
Decomposition Of Intuitionistic Fuzzy Primary Ideals Of ℾ-Rings
-
On Tensor Product of c-Spaces
-
Hardy Spaces and Integral Means of Certain Integral Operators on Analytic Functions
-
Fusion frame and its alternative dual in tensor product of Hilbert spaces
-
Alternating quadratic and cubic series with the tail of ln 2
-
On a useful lemma that relates quasi-nonexpansive and demicontractive mappings in Hilbert spaces